机器学习基石听课笔记01
使用场景:
- 无法写出程序
- 探索火星
- 无法轻易定义解决方案
- 语音、视频识别
- 需要作出快速决策
- 高频交易
- 大规模群体下以用户为中心
- 精准营销
机器学习完整定义 在给定已知资料(样本)基础上,通过在假设的函数空间中训练,得到接近f的映射函数
2.1 感知器假设空间
D 训练样本 H 假设空间 f 未知函数 g 近似函数 A 学习算法
通过训练样本D 使用A在假设空间H中选取近似函数g
感知器假设的向量形式: $$ \begin{align*}
h(x)& = sign((\sum_{i=1}^d W_{i}X_{i})-threshold)
&= sign((\sum_{i=1}^d W_{i}X_{i})+\underbrace{(-threshold)}{w_0}·\underbrace{(+1)}{x_0})
&= sign(\sum_{i=0}^d W_{i}X_{i})
&= sign(W^TX)
\end{align*}
$$
所以近似函数其实是一条直线,用向量内积的形式表示,直线上的点满足$W^TX=0$,两侧的点分别大于0,小于0.我们训练的过程其实是不断调整法向量W,使法向量所确定的直线完美划分不同样本。(直线的向量表示)
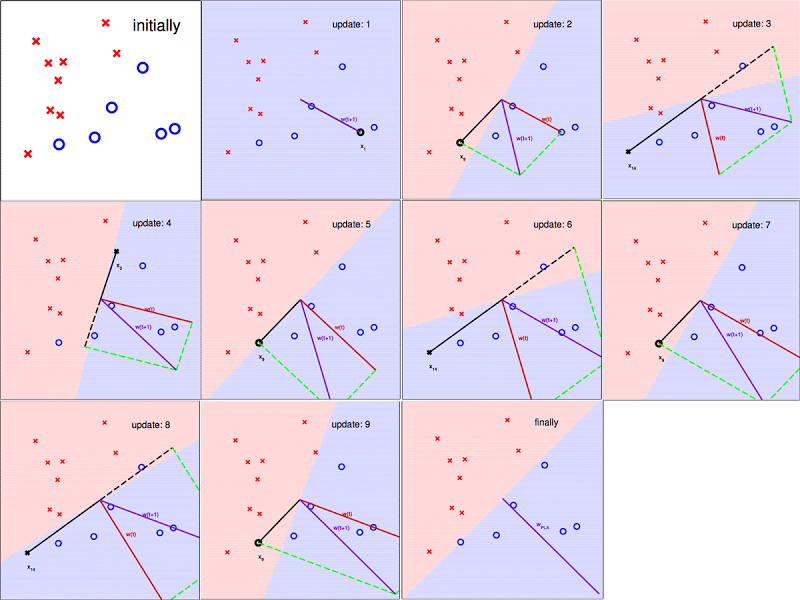
2.2 感知器学习算法PLA
目标函数:$y = sign(np.dot(W^T,x))$ y = np.dot(Wt,x) 其实是向量内积 当两个向量垂直时,结果为0,大于0时向量夹角为锐角。
初始化:$W_0=X_0$
更新过程:寻找不满足分类的点$X_m$,
y为标签值。当标签值为-1,而实际预测为1时,W与X的夹角是锐角,需要W-X使得W与X成钝角,从而修正W向量;当标签值为1,而实际预测为-1时,W与X的夹角是钝角,需要W+X使得W与X成锐角,从而修正W向量;
2.3 PLA 证明
PLA收敛性: