The Unreasonable Effectiveness of Recurrent Neural Networks
from:http://karpathy.github.io/2015/05/21/rnn-effectiveness/
VNN和卷积网络的限制:
- 接受固定长度的向量作为输入(例如一张图片),并产生固定长度的向量作为输出(例如不同类别的概率)。
- 使用固定数量的概念步骤去执行这些映射(例如模型的层数)
递归网络的优势:
允许我们在向量序列上进行操作,输入序列、输出序列。
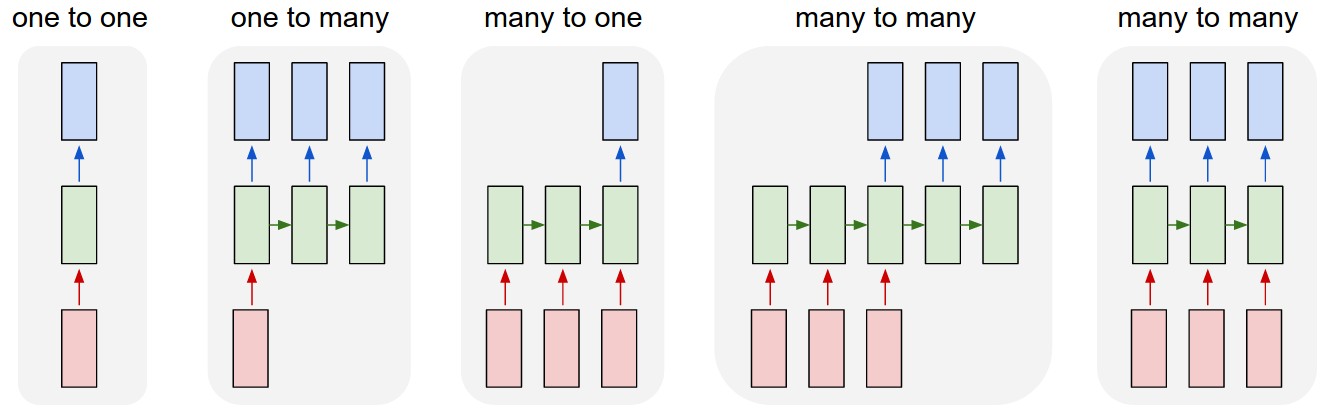
每个长方形都是一个向量,箭头代表函数(例如矩阵乘法)
绿色代表RNN的state。
从左到右:
- 不含RNN的Vanilla模式,固定长度的输入和固定长度的输出,例如图像分类;
- 序列输出,例如捕获图像转换为一句话输出
- 序列输入,例如情感分析,输入一段话,判断是积极还是消极
- 序列输入和序列输出,例如机器翻译
- 同步输入序列和输出序列,例如对视频的每个frame帧打标签
在任意情况下,序列的长度都没有预先指定的约束,因为(绿色)递归转换是固定的,并且可以多次调用。
与通过固定步骤的固定网络相比,操作的顺序机制显然更为强大。RNN通过固定的函数(可学习进化)结合输入向量和状态向量并产生新的状态向量。可以理解为通过给定的输入和一些中间变量执行某个函数。RNN本质上是对程序的描述,并被认为是图灵完备的,因为他们可以通过合适的权重来反正任意程序。
如果vanilla神经网络是对函数的优化 那训练神经网络是对程序的优化。
RNN
-
RNN计算
class RNN: # ... def step(self, x): # update the hidden state self.h = np.tanh(np.dot(self.W_hh, self.h) + np.dot(self.W_xh, x)) # compute the output vector y = np.dot(self.W_hy, self.h) return y三个参数:W_hh,W_xh,W_hy
隐含状态:self.h
np.dot:矩阵相乘,np.tanh:对矩阵中的每个元素进行计算(注意到tanh的输入是两个矩阵相加,一个矩阵与隐藏状态有关,另一个矩阵与输入参数有关)
训练方法:我们用随机数对RNN的矩阵进行初始化,训练过程中的大部分工作都是寻找产生理想行为的矩阵,采用的方法是使用loss function
-
深度RNN
使用多个RNN 一个RNN的输出作为另外一个输入,事实上就是向量的输入和输出,以及在反向传播流经每个module的梯度变化。
-
LSTM
在实际中,更倾向用LSTM而不是RNN,因为LSTM更新函数更为优秀,更有吸引力的反向传播变量。LSTM与RNN相似,除了更新函数不一样。
####激活函数
-
sigmoid函数:$f(x) = \frac{1}{(1+e^{-x})}$ 值域为(0,1)导数为$f’(x) = f(x)*[1-f(x)]$
-
tanh函数:$tanh(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}}$
这个公式用代码实现会overflow,因为$e^x$会无穷大 $$ tanh(x) =\begin{equation}
\begin{cases}
\frac{1-e^{-2x}}{1+e^{-2x}}, & x>0 \
\frac{e^{2x}-1}{e^{2x}+1}, & x<0 \
\end{cases}
\end{equation} \
这个公式用代码实现不会overflow,因为e^{-x}\in (0,1) $$
- ReLU函数:$ReLU(x) =max(0,x)$
- 速度快,计算代价很小
- 减轻梯度消失问题
- 稀疏性,更低的激活率
以上是三种主要的激活函数。